[기타] 소수(prime number)의 개수
18.10.13 01:38
| 3,872 hit
리만가설은 소수의 분포와 관련이 있다. 특정 자연수 이하의 소수의 개수와 관련이 있다. 소수는 겉보기에는 무작위한 것처럼 보이지만 이리저리 변형을 하면 특이한 규칙들이 나온다.
소수를 걸러내는 알고리즘 중에 가장 단순한 것이 에라토스테네스의 체라는 방식이다. 소수로 나누어지는 모든 수를 빼면 결국 자연수에 소수만 남게 하는 방식이다. 2부터 시작해서 2의 배수가 되는 모든 자연수를 제외한다. 그 다음 3부터 시작해서 3의 배수가 되는 모든 자연수를 제외한다.....
이 방식으로 10의 9승까지 소수를 계산하는데 시간이 좀 걸렸지만 가능했고, 10의 10승까지 계산하려고 했더니 32기가 메모리가 부족해서 프로그램이 멈췄다.
에라토스테네스의 체 알고리즘은 간단하다. 2부터 n까지의 자연수가 있을 때 모든 자연수를 검사하는 것이 아니라 n 제곱근까지만 검사하면 된다. n 제곱근이 넘어가면 n 보다 큰 수가 되기 때문이다. 이렇게 계산을 하면 n 제곱근보다 작은 소수와 n 제곱근보다 큰 소수가 나온다. 이미 알려진 것인지는 모르겠지만, 여기에 좀 특이한 규칙이 있다는 것을 발견했다.
1. n 제곱근보다 작은 소수의 개수
2. n 제곱근보다 큰 소수의 개수
이렇게 두 가지 파트로 나눌 수 있는데, 에라토스테네스의 체 방식에 의하면 계산 과정이 1에서 끝난다. 즉, 2는 1과정의 결과로서 결정이 되는 것이다. 예를 들어보자.
2부터 10까지의 수를 체크해보자. 10의 제곱근(정수부분만 취함)까지 계산하면 10 안에 있는 모든 소수를 추려낼 수 있다.
√10 = 3.1622 에서 3 까지 체크 함.
2 와 3이 소수가 됨을 알 수 있고 그 결과로 √10 보다 큰 7이 소수로 남게 된다. 7은 7보다 큰 수를 직접 나눠서 소수인지 여부를 가릴 필요가 없다.
2부터 1000까지의 수를 체크해보면
√1000 = 31.622 에서 31 까지 체크 함.
31 이하 소수의 개수는 11 개다: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31
31 보다 크고 1000 보다 작은 소수의 개수는 157 개다.
2 ~ 1000 사이에 있는 소수의 총 개수는 168 개다.
11개의 소수만으로 2 부터 1000 사이에 있는 모든 소수의 개수를 알아낼 수 있다.
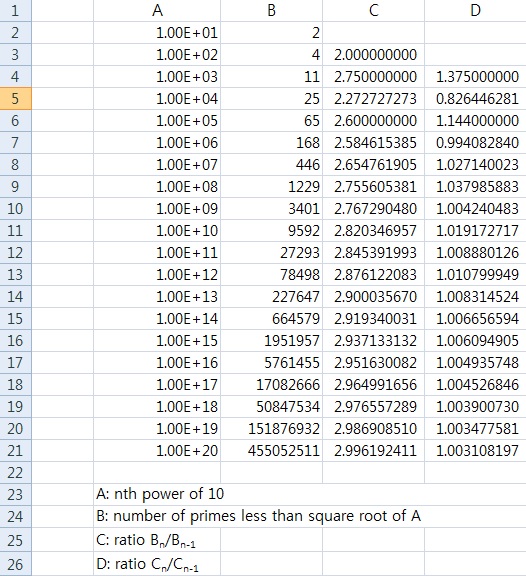
소수를 찾으려는 최대 범위를 n 이라 하면, n 제곱근 이하의 소수의 개수와 n 보다 작은 소수의 개수 간에 어떤 상관 관계가 있는지 체크해 보았다.
n a b
--------------------------
1e+1 2 4
1e+2 4 25
1e+3 11 168
1e+4 25 1229
1e+5 65 9592
1e+6 168 78498
1e+7 446 664579
1e+8 1229 5761455
1e+9 3401 50847534
n : 자연수 범위
1e+1 : 10의 1승
1e+2 : 10의 2승
1e+3 : 10의 3승
a : n 제곱근보다 작은 소수의 개수
b : n 보다 작은 소수의 개수
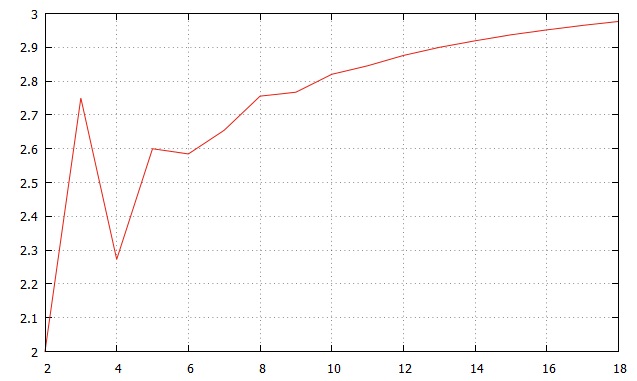
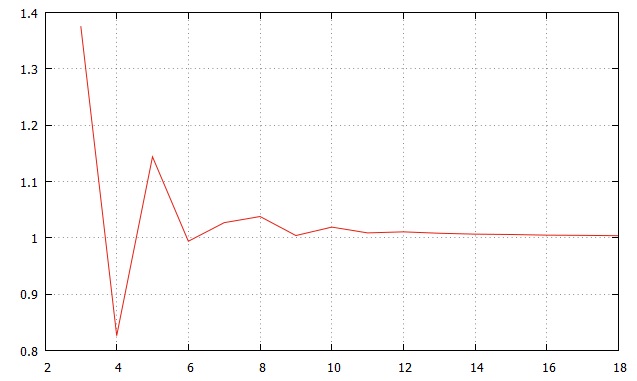
여기서 규칙성이 보인다. b 에 나타나는 개수가 모두 a 에도 나타난다. 그런데 순서대로 나타나는 것이 아니라, 자연수 범위가 1승 증가할 때마다 b 에 나타는 개수와 그 다음 개수 사이에는 없는 새로운 개수가 a 에 나타난다.
10의 10승을 계산하려다가 메모리 부족으로 프로그램 멈추었지만, 이것이 만약 규칙적이라면 10의 10승의 제곱근보다 작은 소수의 개수는 9592 개가 될 것이다.
이 관계가 이미 알려진 것인지는 모르겠다. a 와 b 간에 어떤 관계가 있는지 어떤 의미가 있는지는 모르겠다.